Chapter - Algorithm with Math
Math in Programming
우리가 사용하는 컴퓨터는 0과 1로 모든 연산을 실행한다.
컴퓨터가 단순하게 연산하기 때문에, 기본적인 컴퓨터 과학과 수학은 통하는 부분이 있다.
그러므로 수학을 학습하는 것은 프로그래밍의 기본을 탄탄히 하는 일이다. 그러므로 수학은 프로그래밍에 많은 도움이 된다.
Algorithm with Math
알고리즘 문제를 풀 때 가장 먼저 해야 할 것은 무엇일까? 문제를 이해하고 어떻게 풀 것인지 전략을 세우는 것이다. 문제 풀이를 위해 전략을 세우지 않는다면, 어떤 자료구조를 사용할지, 어떤 알고리즘 기법을 사용할지 판단할 수 없다. 최근 코딩 테스트에 등장하는 알고리즘 문제는 단순히 "너 이 알고리즘 알아?"라고 묻지 않는다. 요즘 출제되는 문제는 "특정 방법을 사용해서 풀어볼래?"라고 물어보는 문제가 자주 등장한다. 이때 "특정 방법을 사용해서 풀어 볼래?"라는 질문은 수학적 사고 능력, 다시 말해 "컴퓨팅 사고를 할 수 있어?라고 물어보는 것과 같다. 따라서, 수학적 사고를 통해 컴퓨팅 사고를 할 수 있어야 한다.
다양한 수학적 개념이 있지만, 알고리즘 문제와 코딩 테스트에 자주 등장하고 필요한 주요 개념들만 학습한다. 크게 3가지 개념 GCD/LCM(최대공약수, 최소 공배수), 순열/조합, 멱집합을 간단히 소개하고, 문제를 풀면서 활용한다. 이를 통해 어떤 문제에서 어떤 수학적 개념이 필요한지 파악하는 연습을 한다.
우리는 수학이라는 학문을 공부하는 것이 아니라, 문제가 어떤 수학적 개념을 요구하는지 파악해야 한다. 따라서 당장 코드를 작성하지 않고, 여러 가지 상황을 먼저 접해 본다. 그리고 나서 각 수학 개념에 관련된 문제를 코드로 구현한다.
Algorithm with Math - 순열/조합
문제: 카드 뽑기
[A, B, C, D, E]로 이우러진 5장의 카드가 있습니다. 이 5장의 카드 중 3장을 선택하여 나열하려고 한다. 이때, 다음의 조건을 각각 만족하는 경우를 찾아야 합니다.
- 순서를 생각하며 3장은 선택합니다.
- 순서를 생각하지 않고 선택합니다.
각 조건을 만족하면서 카드를 나열하는 방법은 모두 몇 가지인가요?
조건 1을 만족하는 모든 경우의 수
1번 조건에서 모든 경우의 수를 구할 때에는 모든 카드를 1장씩 나열하면서 나열된 카드가 3장에 도달하면 카드의 나열을 중지한다.
1번의 조건을 만족하려면, 다음과 같은 방법으로 경우의 수를 구한다.
- 첫번째 나열하는 카드를 선택하는 방법에는 다섯 가지가 있다.
- 첫번째 카드를 나열하고 난 다음, 두번째 카드를 선택하는 방법은 네 가지가 있다.
- 두번째 카드를 나열하고 난 다음, 세번째 카드를 선택하는 방법은 세 가지가 있다.
따라서 5 * 4* 3 = 60 가지의 방법이 있다.
이렇게 n개 중에서 일부만을 선택하여 나열하는 것을 순열이라고 한다. 순열은 순서를 지키며 나열해야 한다. 예를 들어 카드를 3장 뽑을 때, [A, B, D]와 [A, D, B] 두 경우 모두 A, B, D라는같은 카드를 3장 선택했지만, 나열하는 순서가 다르므로 서로 다른 경우로 파악해야 한다.
순열을 일반화 과정을 거쳐, Permutation의 약자 P로 표현한다.
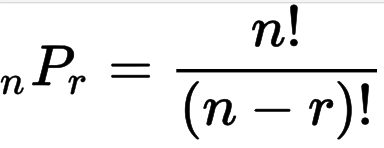
- 5장에서 3장을 선택하는 순간 모든 순열의 수 = 5P3 = (5 * 4* 3* 2 * 1) / (2 * 1) = 60
- 일반식 : nPr = n! / (n - 1)
- ! 은 팩토리얼(factorial)로 n!은 n에서부터 1씩 감소하여 1까지의 모든 정수의 곱이다.(n보다 작거나 같은 모든 양의 정수의 곱이다.)
- 5! = 5 * (5 - 1) * (5 - 2) * (5 - 3) * (5 - 4) = 5 * 4 * 3 * 2 * 1 = 120
- 팩토리얼에서 0!과 1!은 모두 1이다.
조건 2를 만족하는 모든 경우의 수
2번 조건에서 모든 경우의 수를 구할 때는 3장을 하나의 그룹으로 선택히야 한다. 2번의 조건을 만족하려면, 다음과 같은 방법으로 경우의 수를 구한다.
- 순열로 구할 수 있는 경우를 찾는다.
- 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눈다.
먼저, 조합은 순열과 달리 순서를 고려하지 않는다. 만약 순열처럼 순서를 생각하여 경우의 수를 센다면, 조합으로써 올바르지 않을 것이다. 예를 들어 [A, B, C], [A, C, B], [B, A, C], [B, C, A], [C, A, B], [C, B, A]의 여섯 가지는 모두 다른 경우로 취급하지만, 조합에서는 이 여섯 가지를 하나의 경우로 취급한다. 다시 말해 순열에서처럼 순서를 생각하여 선택하면, 중복된 경우가 6배 발생한다.
여기서 나온 여섯 가지 경우의 수는 3장의 카드를 순서를 생각하여 나열한 모든 경우의 수이다. 3장의 카드를 순열 공식에 적용한 결과가 3! / (3 - 3)! = (3 * 2* 1) / 1 = 6 이다. 순서를 생각하느라 중복된 부분이 발생한 순열의 모든 가짓수를, 중복된 6가지로 나우어 주면 조합의 모든 경우의 수를 얻을 수 있다.
따라서 (5 * 4 * 3 * 2 * 1) / ((3 * 2 * 1) * (2 * 1)) = 10 이다.
조합은 일반화 과정을 거쳐, Combination의 약자 C로 표현한다.
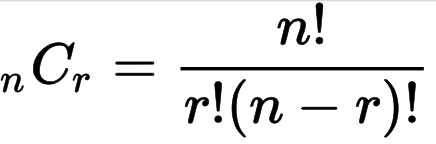
- 5장에서 3장을 무작위로 선택하는 조합에서 모든 경우의 수 = 5C3 = 5! / (3! * 2!) = 10
- 일반식: nCr = n! / (r! * (n - r)!)
문제: 소수 찾기
한 자리 숫자가 적힌 종잇조각이 흩어져 있습니다. 흩어진 종잇조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다. 종이에 기록된 모든 숫자가 배열로 주어진다면, 이 종잇조각으로 만들 수 있는 소수는 몇 개인가요?
이 문제에는 순열이 숨어있다. 만약 이 사실을 알아차린다면, 문제를 보다 쉽게 해결할 수 있다. 순열을 이용한다면, 다음과 같이 전략을 세울 수 있다.
- n개의 숫자 중에 1 ~ k 개를 뽑아서 순열을 생성한다.
- 각 순열을 정수로 변환하고, 해당 정수가 중복되지 않으면서 동시에 소수인지 검사한다.
- 소수이면 개수를 센다.
숫자는 순서에 의해 전혀 다른 값이 될 수 있다. 예를 들어 123과 321은 전혀 다른 숫자다. 만약 이 문제를 조합으로 접근하게 된다면, 123과 321은 같은 경우로 취급한다. 따라서, 순서를 고려하지 않고 k 개를 뽀아내는 조합으로는 이 문제를 해결할 수 없다.
문제: 일곱 난쟁이
왕비를 피해 일곱 난쟁이와 함께 평화롭게 생활하고 있던 백설 공주에게 위기가 찾아왔습니다. 하루일과를 마치고 돌아온 "일곱" 난쟁이가 "아홉"명이었던 겁니다. 아홉 명의 난쟁이는 모두 자신이 "백설 공주와 일곱 난쟁이"의 주인공이라고 주장했습니다. (뛰어난 수학적 직관력을 가지고 있던) 백설 공주는 일곱 난쟁이의 키의 합이 100임을 기억해냈습니다. 아홉 난쟁이의 가각의 키가 주어질 때, 원래 백설 공주와 평화롭게 생활하던 일곱 난쟁이를 찾는 방법은 무엇인가요?
위 문제는 조합을 이용해서 일곱 난쟁이를 찾을 수 있다. 모든 일곱 난쟁이의 키를 합했을 때 100이 된다고 주어졌기 때문에, 9명의 난쟁이 중 7명의 난쟁이를 순서를 생각하지 않고, 난쟁이 7명의 키를 합했을 때 100이 되는 경우를 찾으면 된다.
Algorithm with Math - GCD / LCM
- 약수: 어떤 수를 나누어떨어지게 하는 수
- 배수: 어떤 수의 1, 2, 3, ...n 배하여 얻는 수
- 공약수: 둘 이상의 수의 공통인 약수
- 공배수: 둘 이상의 수의 공통인 배수
- 최대 공약수(GCD. Greatest Common Divisor): 둘 이상의 공약수 중에서 최대인 수
- 최소 공배수(LCM. Least Common Multiple): 둘 이상의 공배수 중에서 최소인 수
문제: Mask States
방역용 마스크를 제작/판매하는 Mask States 사는 이례적인 전염성 독감 예방으 ㄹ위해 기존 가격을 유지하며 약속된 물량의 방역용 마스크를 제공하고 있습니다. 이 회사는 사장을 포함하여 A, B, C 세 명뿐이고, 이들 모두 마스크를 제작합니다. 각각의 제작 속도는 다음과 같습니다.
A는 55분마다 9개를, B는 70분마다 15개를, C는 85분마다 25개의 방역용 마스크를 만들 수 있습니다. 이 회사의 사람들은 05:00 시부터 동시에 마스크를 만들기 시작하여 각 55분, 70분 85분 동안 연속으로 마스크를 제작한 후, 5분씩 휴식을 취합니다. 이들 세 명이 청므으로 동시에 쉬는 시점이 퇴근 시간이라면, 이날 하루에 제작한 마스크는 모두 몇 개인가요? (휴식시간과 퇴근시간이 겹치는 경우, 휴식을 취한 뒤 퇴근합니다.)
풀이 방법은 다양하다. 그러나 이 문제에서 최소 공배수를 떠올릴 수 있다면, 더 쉽고 빠르게 문제를 해결할 수 있다.
A, B, C의 작업 시간과 쉬는 시간 5분을 더하면 A, B, C는 각각 60분, 75분, 90분마다 마스크를 만든다. 세명이 동시에 휴식을 취하는 시점은 세 명이 쉬고 난 직후가 같은 시점이 된다. 따라서 쉬고 난 직후가 처음으로 같은 시점을 구해야 하므로 공배수와 최소 공배수의 개념을 알아야 한다.
결과적으로, LCM(60, 75, 90)은 900이다.(LCM; Least Common Multiple, 최소 공배수)
따라서 A는 B, C와 휴식을 취한 직후가 처음으로 같은 시점까지 900/60 = 15 번 작업하고, 15 * 9개 = 135개의 마스크를 만들어 낸다.
B는 900/75 = 12번의 작업을 반복하고 12번 * 15개 = 180개,
C는 900/90 = 10번의 작업을 반복하고 10번 * 25개 = 250개의 마스크를 만들어 낸다.
따라서, A, B, C가 하루에 제작한 마스크의 총 개수는 135개 + 180개 + 250개 = 565개가 된다.
이렇게 기본적인 수학 개념은 프로그래밍 문제를 해결하는데 큰 도움이 된다. 그리고 문제의 답이 도출해 내는 것보다, 해당 문제에서 최대 공약수와 최소 공배수를 활용해야겠다는 문제 해결 전략을 세우는 것이 가장 중요하다.
문제: 조명 설치
코드스테이츠 라운지에 있는 가로 24cm, 세로 12cm인 직사각형 모양 조형물의 가장자리에 조명을 설치하려고 합니다. 네 모퉁이에는 조명을 반드시 설치해야하고, 나머지 조명은 일정한 간격으로 설치하려고 할 때, 필요한 최소한의 조명 개수는 몇 개일까요? 이때, 꼭지점을 제외한 직사각혀의 모든 변에는 최소 하나 이상의 조명이 반드시 설치되어야 합니다. (단, 설치한 조명의 간격은 정수로 이루어진 cm 단위입니다.)
이 문제의 답은 12개이다.
이 문제에서 필요한 전구의 개수를 구하려고 할 때, 최대 공약수를 떠올리면 빠르게 문제를 해결할 수 있다. 그러나 간단한 문제를 풀더라도 훈련하지 않으면, 최대 공약수라는 수학적 개념을 바로 떠올리는 것은 결코 쉬운 일이 아니다. 계속해서 문제를 접하고 문제를 해결하기 위해 필요한 수학적 개념을 떠올리 수 있도록, 반복해서 연습해야 한다.
이 문제를 해결해 보자. 모든 조명을 일정한 간격으로 설치해야 하므로, 가변과 세로변의 공약수를 구해야 한다.
가로와 세로 각각 나우어서 나머지가 없이 떨어지는 수들을 나열한 뒤, 공통된 수만 모이면 공약수를 구할 수 있다. 그리고 공약수를 기준으로 조명을 설치하면 길이가 다른 가로와 세로여도 일정하 간격으로 나누어 조명을 설치할 수 있다.
최소로 필요한 조명의 개수를 파악해야 하기 때문에 최대 공약수가 필요하다. 따라서 GDC(12, 24)는 12이고 네 모퉁이는 반드시 설치해야 하므로 각 변의 길이를 최대 공약수 12로 나누어 최소로 필요한 조명의 개수를 구할 수 있다. (GCD; Greatest Common Divisor, 최대 공약수)
(12 / 12 + 24 / 12) * 2 = 3 * 2 = 6개
그러나 이 문제에서는 꼭지점을 제외한 직사각형의 모든 변에, 최소 하나 이상의 조명이 설치되어야 하므로 12를 제외한 최대 공약수로 문제를 해결해야 한다.
(12 / 6 + 24 / 6) * 2 = 6 * 2 = 12개
이렇게 알고리즘 문제나 코딩 테스트에서는 여러 가지 상황을 제시하고, "특정 방법을 사용해서 풀어 볼래?"라는 의도로 문제를 제출한다. 그리고 이 문제를 해결하기 위해서는 수학적 개념을 사용해야 하는 경우가 종종 있다.
'TIL > Code States' 카테고리의 다른 글
| Code States 52일차 - [데이터베이스] 관계형 데이터베이스 (0) | 2021.10.08 |
|---|---|
| Code States 52일차 - [데이터베이스] 관계형 데이터베이스 (0) | 2021.10.08 |
| Code States 50일차 - [자료구조/알고리즘] 코딩 테스트 준비 (0) | 2021.10.06 |
| Code States 49일차 - [Linux] 심화 (0) | 2021.10.05 |
| Code States 44일차 - 클라이언트 빌드와 배포 (0) | 2021.09.28 |